Fluctuating Spin g-tensor in Small Metal Grains
The ground state of a small metal particle with an odd number of electrons is required by quantum mechanics to be doubly degenerate (Kramer's degeneracy). Application of a weak magnetic field B splits the degeneracy linearly, by an amount g 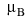 B, which is observable in experiments that measure the addition spectrum for electrons tunneling onto the particle. For a material such as gold, with strong spin-orbit scattering, the value of g may be reduced considerably relative to the value
B, which is observable in experiments that measure the addition spectrum for electrons tunneling onto the particle. For a material such as gold, with strong spin-orbit scattering, the value of g may be reduced considerably relative to the value 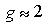 which holds for free electrons, and may vary in a chaotic way from one energy level to another in a particle. (This may be contrasted with the value
which holds for free electrons, and may vary in a chaotic way from one energy level to another in a particle. (This may be contrasted with the value 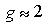 which is observed in spin-resonance experiments in Au films.)
which is observed in spin-resonance experiments in Au films.)
The value of g depends on the direction of the applied magnetic field, and may be written as 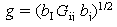 where b is a unit vector in the direction of B, and G is a symmetric tensor characteristic of the energy level. The three eigenvalues of G are nonnegative, and may be denoted
where b is a unit vector in the direction of B, and G is a symmetric tensor characteristic of the energy level. The three eigenvalues of G are nonnegative, and may be denoted 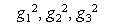 where
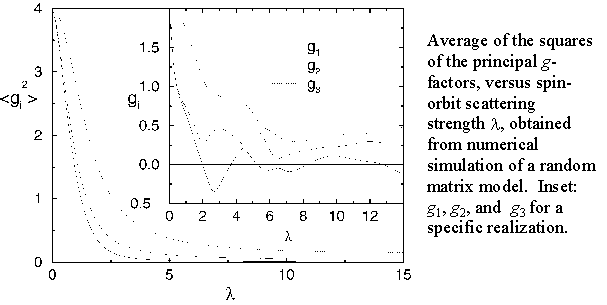
where 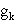 are the "principal g-values" of the energy level. We show that with no loss of generality, any two of these value may be chosen to be positive; however, the sign of the third is then determinable, at least in principle, by a spin resonance experiment, and can be positive or negative. We have calculated analytically the joint probability distribution for the three principal values, in the case of strong spin-orbit scattering, and have obtained numerical results for typical g-values and for the mean g-value, for intermediate values of the spin-orbit scattering.
are the "principal g-values" of the energy level. We show that with no loss of generality, any two of these value may be chosen to be positive; however, the sign of the third is then determinable, at least in principle, by a spin resonance experiment, and can be positive or negative. We have calculated analytically the joint probability distribution for the three principal values, in the case of strong spin-orbit scattering, and have obtained numerical results for typical g-values and for the mean g-value, for intermediate values of the spin-orbit scattering.
P.W. Brouwer, X. Waintal, and B.I. Halperin, Phys. Rev. Letters 85, 369 (2000).
Halperin
Harvard MRSEC (DMR-0820484)
