Crumpling Soda Cans: Predicting the Stability Landscape of Shell Buckling

Crushing a soda can from top to bottom is easier if it is dented initially on the side. Predicting the force needed to crush a dented can, however, which is of critical importance for structural reliance of materials engineering is quite challenging.

A team at the Harvard MRSEC led by Rubinstein, Hutchinson, and Brenner investigated the crumpling of soda cans by controlling the denting and applied force until they buckled with a loud snap.

Through their systematic study of the axial denting and applied forces, they were able to map out a "stability landscape," to understand the conditions where shell cylinders will buckle from instabilities. Because of the sudden-onset effect they were able to predict the response from soda cans to a more general universal behavior for cylindrical objects. Thus, researchers can use this stability map to predict the strength of a space rocket or other similar objects to a gentle poke from the side (adapted from Katherine Wright, contributing editor for Physics).

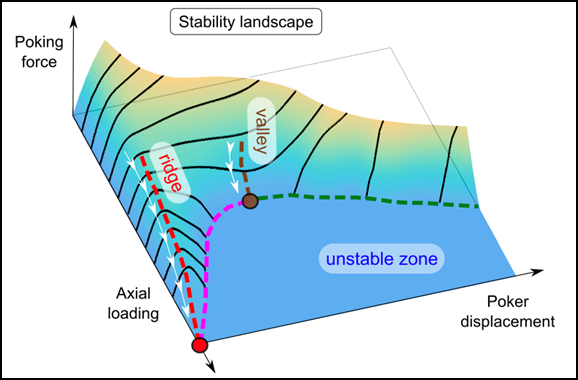
A team at the Harvard MRSEC led by Rubinstein, Hutchinson, and Brenner investigated the response and stability of cans when subjected to lateral poking with a point probe. The force-displacement curves of the probe at different axial loads unveil a rich landscape in the three-dimensional phase space spanned by axial load, poker displacement and poker force. This landscape fully characterizes the stability of perfect shells and imperfect ones in the case where a single defect dominates. Tracking ridges and valleys of this landscape defines a natural phase-space coordinates for describing the stability of shells.

A previous NSF-MRSEC Highlight

Publication:
E. Virot, T. Kreilos, T. M. Schneider, S. M. Rubinstein, "Stability landscape of shell buckling," Phys. Rev. Lett. 119, 224101 (2017)